
In contrast to strict inequalities, there are two types of inequality relations that are not strict: These relations are known as strict inequalities, meaning that a is strictly less than or strictly greater than b.

There are several different notations used to represent different kinds of inequalities: It is used most often to compare two numbers on the number line by their size.

In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. Let’s first write down the comparison with the greater than or equal to operator.The feasible regions of linear programming are defined by a set of inequalities. Solved Example: If x is greater than or equal to 25 and y is less than or equal to 40, then which one of the following is always correct?
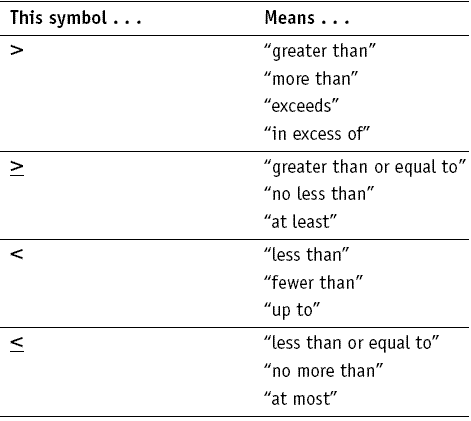
Here are some solved examples of Greater than or Equal to for you to prepare for your exam. Solved Examples on Greater than or Equal to 3 ≥ clothes.Ĭheck out this article on Arithmetic Mean. So we can use the greater than or equal to sign here i.e. You also need to pack at least 3 pairs of clothes. We use the ≤ symbol for inequalities like ‘less than or equal to.’ It is the opposite of greater than or equal to meaning not greater than or equal to. Furthermore, you are only allowed to bring 1000ml of apple juice on the plane for this journey. We use the < sign for ‘less than’ inequality. Let’s use the example of you going on vacation to better understand it. This is an effective method for remembering which number is higher. Consider each sign as a mouth, which will always swallow the larger of the two numbers being compared. On the other hand, if we need to say that a is less than y, we write a 4. If we need to say that a is greater than b, we write a > b. We use symbols to depict the case to make them easier to understand. In mathematics, we often use the terms greater than, less than, and equal to are to describe the relationship between two mathematical expressions, variables, or entities. Meaning and Symbol of greater than or equal to We can say, v ≥ 3 meaning v is greater than 3, but there’s a possibility that it can be 3. However, if there is an unknown variable, let’s say v and we need to find out its value then ≥ is a possible case. We can never say, 13 ≥ 4 because we know that 13 > 4. The condition of greater than equal to is not applicable for two known numbers. Closed circles are used for numbers that are less than or equal to and greater than or equal to (≤ or ≥).



 0 kommentar(er)
0 kommentar(er)
